이번 포스팅에서는 자료 구조 기본 내용에 대해 정리해 보고자 합니다.
프로그램 개발 시 자료 구조는 현실 세계에 대해 표현하고자 하는 데이터를 효율적으로 저장할 수 있는 구조화 표현이라 할 수 있습니다.
자료 구조의 분류를 살펴보면
크게 선형 구조와 비선형 구조로 나눌 수 있고 선형 구조와 비선형 구조는 각각 아래와 같이 세분화할 수 있습니다.
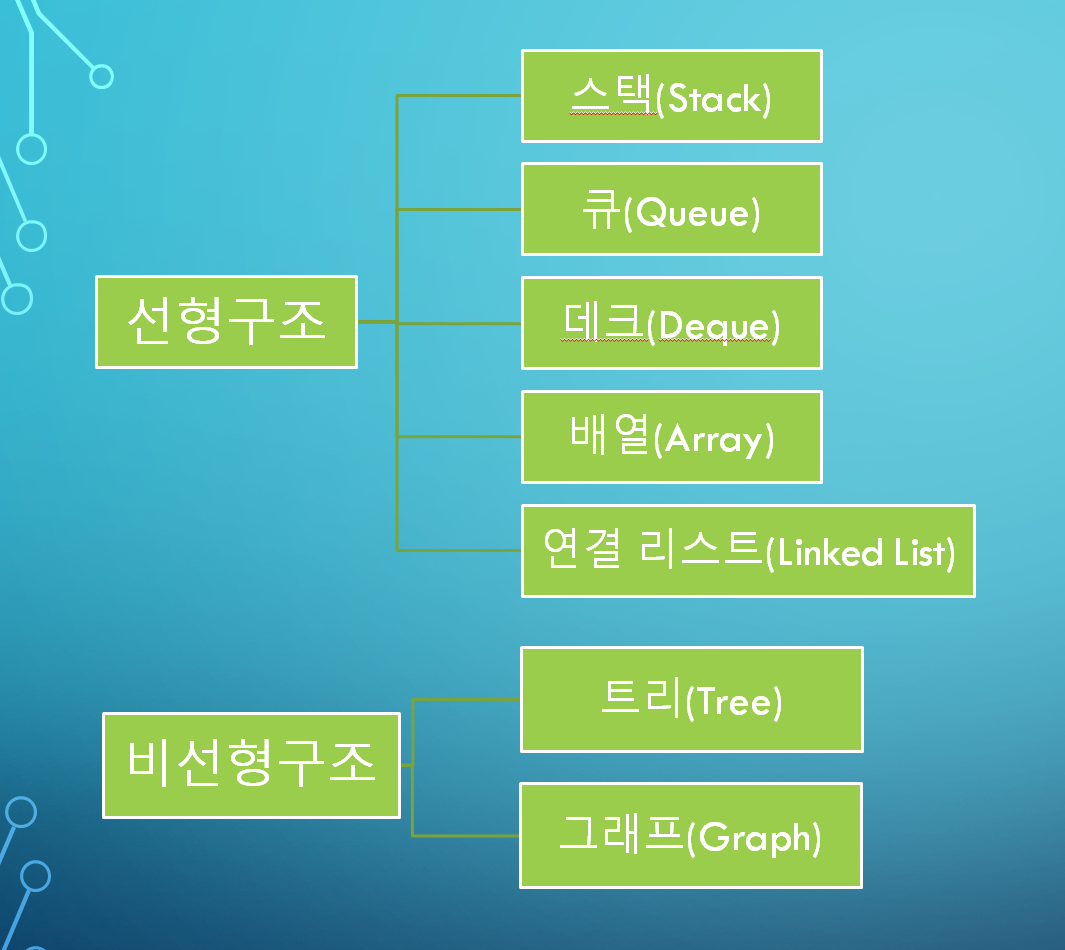
선형 구조를 먼저 살펴보겠습니다.
선형 구조는 데이터와 데이터를 1:1 대응 구조로 관계를 맺어 저장시키는 형태의 자료 구조를 말합니다.
선형 구조 중 스택은 아래의 그림과 같습니다.

스택의 특징은 포인터를 한 개 두고 처음 입력한 데이터가 마지막에 출력되고 마지막에 입력한 데이터가 제일 처음 출력되는 LIFO(Last In First Out) 구조라는 점입니다.
큐는 아래의 그림처럼 삽입과 삭제 포인터 두 개를 두고 한쪽 방향에서는 입력만 하고, 다른 한쪽 방향에서 출력만 하는 구조로 FIFO(First In First Out) 구조가 특징입니다.

큐(Queue)에는 삭제 포인터와 삽입 포인터가 같게 되면 삽입 포인터와 삭제 포인터를 처음 위치로 다시 이동시켜 사용하는 이동 큐(Moving Queue)와 원형 구조로 된 환형 큐(Circular Queue) 등이 있습니다.
데큐(Deque)는 큐 처럼 양쪽에 포인터를 두 개를 사용하는 것은 같지만 각 포인터가 입력과 출력을 할 수 있다는 점에서 큐와 다릅니다. 이름도 Double Ended Queue의 약자로 양쪽 끝에서 입출력이 일어나는 구조입니다.
배열(Array) 구조는 가장 많이 사용하는 자료 구조로 선형 리스트(Linear List), 순서 리스트(Ordered List), 순차 리스트(Sequential List) 등 저장 방식에 따라 약간씩 차이가 있지만 같은 크기의 기억 장소를 연속된 공간에 모아 놓고 원하는 데이터를 기록하거나 액세스 하는 방법은 동일합니다.
다만, 배열에서는 삽입과 삭제시 데이터의 이동이 많이 일어나기 때문에 메모리에 종속적이고 대량의 데이터를 다루기에는 비효율적인 부분이 있다는 점을 기억해야 합니다.
연결 리스트(Linked List)는 데이터를 구성할 때 삽입될 데이터에 포인터를 포함시켜 하나의 데이터 셋으로 구성하고 이 포인터를 이용해서 각 데이터들을 연결하는 형태로 구성하여 저장하는 것을 말합니다.
일명 노드라고 하는 데이터 구조를 통해 데이터 간 링크를 시키고 삽입과 삭제는 링크를 통해 데이터의 이동 없이 링크 부분을 변경하여 연결하거나 단절시킴으로써 삽입과 삭제를 간편하게 처리할 수 있다는 특징이 있습니다.
연결 리스트의 구조를 그림으로 표현하면 아래와 같습니다.

각 노드는 데이터 1개와 링크 주소를 세트로 하여 정보를 담고 있으며 각 노드의 링크는 연결될 다른 노드의 주소 정보를 담고 있습니다. 위 그림은 단일 링크 리스트로 마지막 링크의 값이 없지만 이를 100번지와 연결시키면 단일 환형 링크 리스트가 될 수 있습니다.
다음은 비선형 구조에 대해 살펴보겠습니다.
비선형 구조는 자료와 관계를 맺고 있는 다른 자료가 여러 개 존재할 때, 이 관계를 1:N, N:M 등으로 표현하기 위한 구조를 말합니다.
1:N 구조는 Tree 구조, N:M 구조를 Graph 구조로 나타낼 수 있으며 그래프 구조가 당연히 Tree 구조를 포함하는 개념입니다.
그림으로 보시면 쉽게 이해할 수 있습니다.
트리 구조는 아래의 그림과 같습니다.
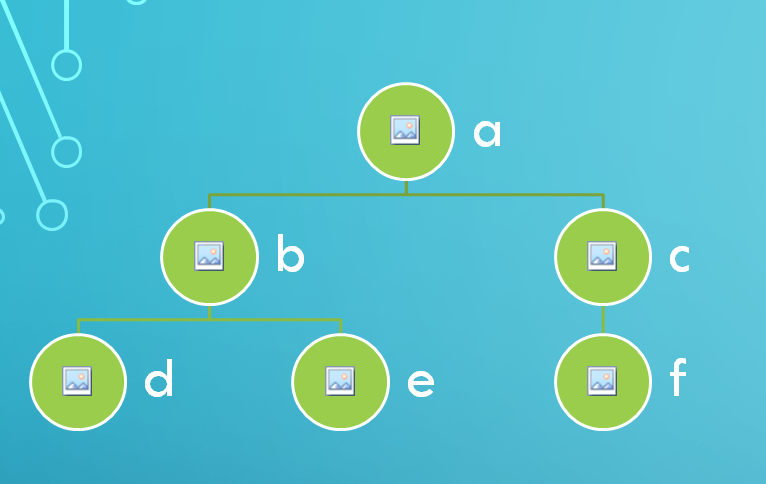
트리구조에서 용어에 대한 이해도 필요합니다.
그림에서 보이는 a는 트리의 뿌리가 되는 노드로 '근노드(Root Node)'라고 부릅니다.
또한 노드 아래에 자식이 없는 노드를 '단노드(Terminal Node)'라고 부르며 그림에서는 d, e, f 노드가 해당됩니다.
반대로 자식이 있는 노드를 '간노드(Nonterminal Node)'라고 부르며 그림에서는 a, b, c에 해당합니다.
차수(Degree)라는 용어도 많이 사용하는데 각 노드에 연결된 가지 수, 즉 자식 노드의 수를 의미합니다.
그래프의 구조는 아래의 그림과 같습니다.
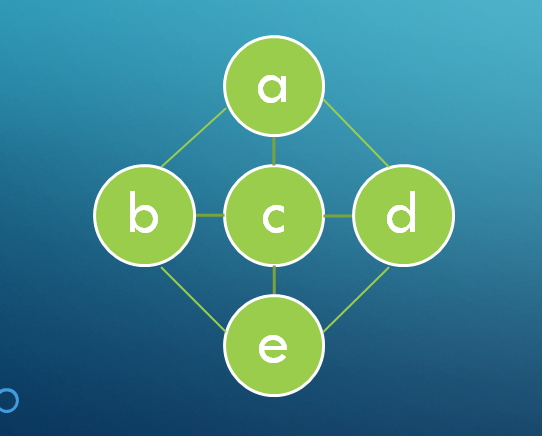
그래프는 임의 관계가 비선형적으로 나타나는 구조를 말하며 최단거리 탐색이나 전자 회로 분석, 통계학 등의 응용 분야에서 많이 활용된다고 합니다.
그래프의 표시는 G = (V, E) 로 표시될 수 있는데 여기서 V는 정점들의 집합을 의미하고 E는 간선의 집합을 의미합니다.
정점은 a, b, c, d를 말하며 간선은 각 정점 사이의 관계로 표현됩니다.
그래프의 표현은 정점과 정점의 관계로 인접 행렬(Adjacency Matrix)로 나타낼 수도 있습니다.
아래의 그림은 a, b, c, d의 그래프를 인접 행렬로 표현한 것입니다.

각 노드간 연결된 관계를 1로 표현하여 인접 행렬로 표현한 그림으로 각 간선의 관계를 표현하고 있습니다.
위 그림은 방향성이 없는 비방향 그래프를 나타낸 것인데 방향성을 나타내면 방향 그래프로 표현할 수 있고
방향성에 가중치(값)을 부여하면 비용 그래프로 나타내어 최소 비용 트리로 나타낼 수도 있습니다.
지금까지 자료 구조에 대해 정리해 보았습니다.
효율적인 자료구조는 프로그램의 성능과도 직결될 수 있기 때문에 잘 정리해 두시면 좋을 것 같습니다.
감사합니다.
'기타 IT 정보' 카테고리의 다른 글
| 소프트웨어 개발 및 문서화 표준 용어 정리(MIL-STD-498) (3) | 2020.06.07 |
|---|---|
| 소프트웨어 라이선스 정리 (0) | 2020.06.03 |
| 알고리즘이란? (0) | 2020.05.30 |
| 스마트폰을 노트북에 연동해서 사용하기[사용자 휴대폰 앱] (0) | 2020.05.28 |
| 가상 테스크톱(한 대의 컴퓨터로 다른 환경 만들어서 사용하기) (2) | 2020.05.22 |



댓글